Calculate movement among polygons • BirdFlowR

Overview

The goal here is to estimate movement among polygons over a defined period of time using a BirdFlow model. The result is square movement matrix where the rows correspond to starting polygons and the columns to ending polygons. Values are the proportion of the total population making each movement, which
can be scaled to represent numbers of birds. Optionally each value can be adjusted by the area of the two associated polygons to get a mean movement per square km.

The initial use case was to create a predictor for a model of avian influenza spread. In the example here the polygons are US States but the variable (polys) and the sole required column name (id) are kept deliberately generic so the code will make sense with any set of polygons.

This will likely be turned into a function but the vignette should remain a useful demonstration of how to work with BirdFlow models.

The approach:

Load model, set start and end times for connectivity window, and set total population.
Download and prepare polygons
Calculate the overlap between active cells in the BirdFlow model and the polygons.
Generate starting distributions for each polygon that represent the portion of the species distribution that is in each polygon at the start of the movement.
Run predict() using distributions and start and end time.
Drop time dimension from result preserving just the end distributions.
Convert the ending distribution from model cells to polygons.
Optionally, multiply by the species’ total population (within the Americas) to convert from proportion of population to estimated number of birds
Optionally, divide by the area of both the starting and ending state to make the estimates per unit area - eliminating the polygon size as a factor in the connectivity. This step is not appropriate for all use cases.

Load model and set parameters

This example uses the American Woodcock dataset from BirdFlowModels which is small and runs fast but isn’t fully vetted for scientific use.

Use load_model() for real work.

bf <- BirdFlowModels::amewoo  # you will likely use load_model() instead
start <- BirdFlowR::lookup_timestep("2024-01-15", bf)
end <- BirdFlowR::lookup_timestep("2024-03-20", bf)
population <- 3500000

Visualize the starting distribution from the model

plot_distr(get_distr(bf, start), bf)

Download and read polygons

Download state boundaries from the U.S. Census, read, and cleanup. Any set of spatial polygons with a defined CRS would work equally well.

If you have a polygon shapefile already you could use polys <- sf::read_sf(shapefile_path) and skip this section.


# Download and unzip state boundaries
url <- "http://www2.census.gov/geo/tiger/TIGER2012/STATE/tl_2012_us_state.zip"
dir <- tempdir()
shp_dir <- file.path(dir, "shapefile")
dir.create(shp_dir)
local_zip <- file.path(dir, basename(url))
utils::download.file(url, destfile = local_zip)
utils::unzip(local_zip, exdir = shp_dir)
shp_path <- list.files(shp_dir, pattern = "\\.shp$", full.names = TRUE)

# Load state boundaries
# Variable names are generic to make sense with any set of polygons.
polys <- sf::read_sf(shp_path)

# Drop non-contigous
to_drop <- c("Hawaii", "Commonwealth of the Northern Mariana Islands", 
             "Puerto Rico", "United States Virgin Islands", "Alaska", "Guam", 
             "American Samoa")
polys <- polys[!polys$NAME %in% to_drop, ]

# Select columns
polys <- polys[ , c("GEOID", "STUSPS", "NAME") ]

Prepare polygons for analysis

Add an id field; in this example it is the state names.
Transform to match the BirdFlow Coordinate Reference System (CRS).
Calculate the area in square kilometers of each polygon (sq_km).
Add centroid coordinates (x, y) in the BirdFlow CRS.


# Add generic "id" column (use state name) 
polys$id <- polys$NAME

# Order by id (optional)
polys <- polys[order(polys$id), ]

# Transform to match the BirdFlow model CRS
polys <- sf::st_transform(polys, crs(bf))

# add sq_km to polygons 
# This assumes the projection is in meters which is true for BirdFlow models
polys$sq_km <- sf::st_area(polys)  / 1000^2  |> as.vector()

# Add centroids (only used for the plotting at end of document)
centroids <- sf::st_centroid(polys[, "geometry"]) |> sf::st_coordinates()
colnames(centroids) <- c("x", "y")
polys <- cbind(polys, centroids)

Calculate overlap between active BirdFlow cells and polygons

Make the overlap matrix. Rows correspond to active cells, and columns to the external polygons. The values are the proportion of the cell that overlaps the polygon.


# Convert active cells to polygons
cell_polys <- rasterize_distr(seq_len(n_active(bf)), bf, format = "terra") |>
 terra::as.polygons() |> 
  sf::st_as_sf()
names(cell_polys)[1] <- "i" # BirdFlow location index "i"

# Intersect cells with polygons
suppressWarnings( # Attribute values assumed to be spatially constant... 
  intersection_polys <- sf::st_intersection(cell_polys, polys) 
)
intersection_polys <- intersection_polys[ , c("i", "id")]
intersection_polys$area <- sf::st_area(intersection_polys)
sq_m_per_cell <- prod(res(bf)) 
intersection_polys$prop_of_cell <- intersection_polys$area / sq_m_per_cell

# Calculate the proportion of each cell that overlaps each polygon
# Rows = active cells, columns = polygons 
overlap <- matrix(0, nrow = n_active(bf), ncol = nrow(polys), 
                  dimnames = list(i = seq_len(n_active(bf)),
                                  id = polys$id))
intersection_polys$row <- match(intersection_polys$i, seq_len(n_active(bf)))
intersection_polys$col <- match(intersection_polys$id, polys$id)                  
row_col_index <- intersection_polys[ , c("row", "col")] |> 
  sf::st_drop_geometry() |> 
  as.matrix()
overlap[row_col_index] <- intersection_polys$prop_of_cell |> as.vector()

Build initial distributions

This essentially clips the initial distribution separately to each polygon while assigning values from boundary cells in proportion to their overlap with the polygon.

Note, a single BirdFlowR distribution is a vector of length n_active(bf) multiple can be stored in a matrix with n_active(bf) rows. The matrix here has a column (distribution) for each polygon in polys.


start_distr <- matrix(get_distr(bf, start), 
                              nrow = n_active(bf), 
                              ncol = nrow(polys), 
                              byrow = FALSE, 
                              dimnames = list(i = NULL, 
                             start_poly = polys$id)) 

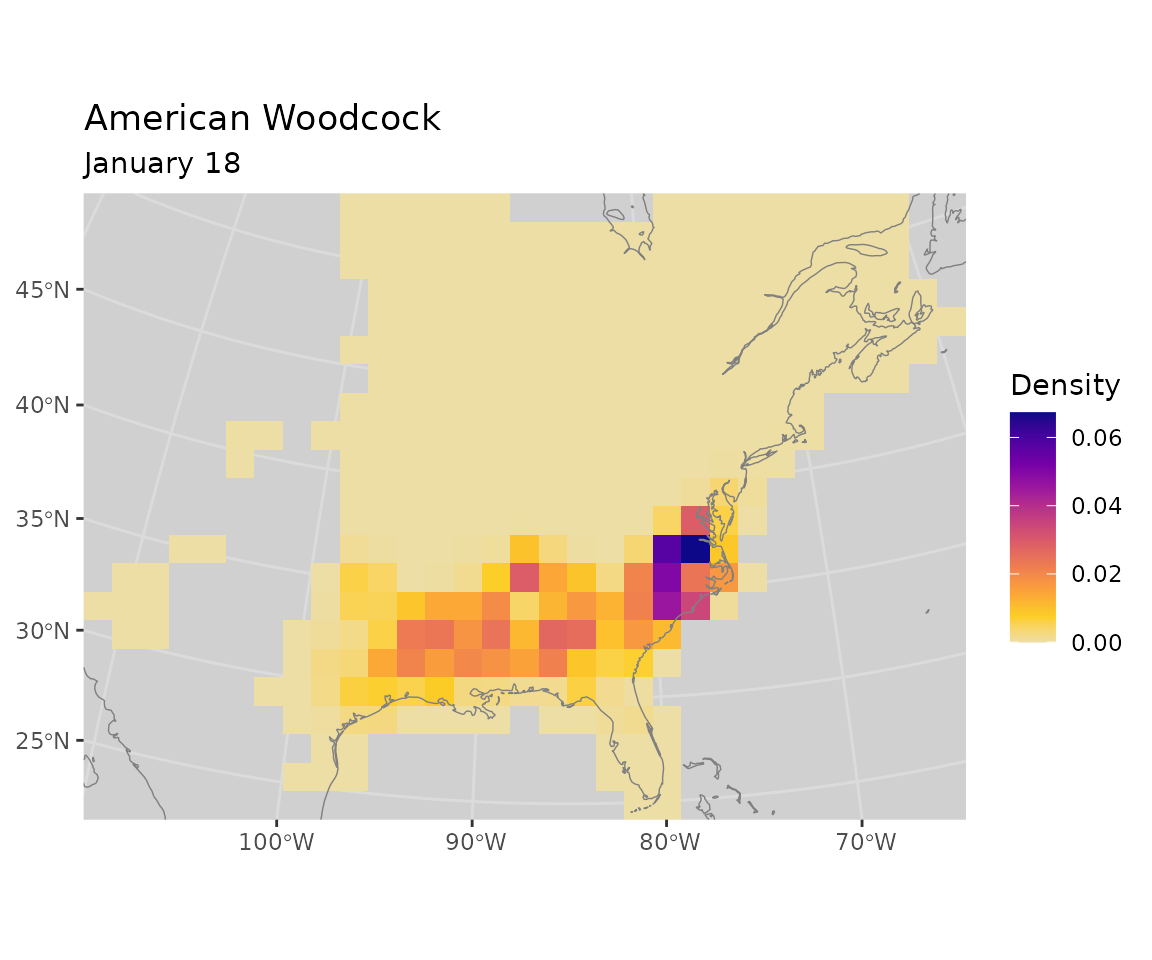
start_distr <- start_distr * overlap

Visualize the distribution for one polygon

Visualize the initial distribution for the polygon with the highest initial abundance (North Carolina).

sel <- which.max(apply(start_distr, 2, sum))
plot_distr(start_distr, bf, subset = sel) + 
  ggplot2::geom_sf(data = polys, 
                   inherit.aes = FALSE, 
                   linewidth = 0.2, 
                   color = "black", 
                   fill = NA)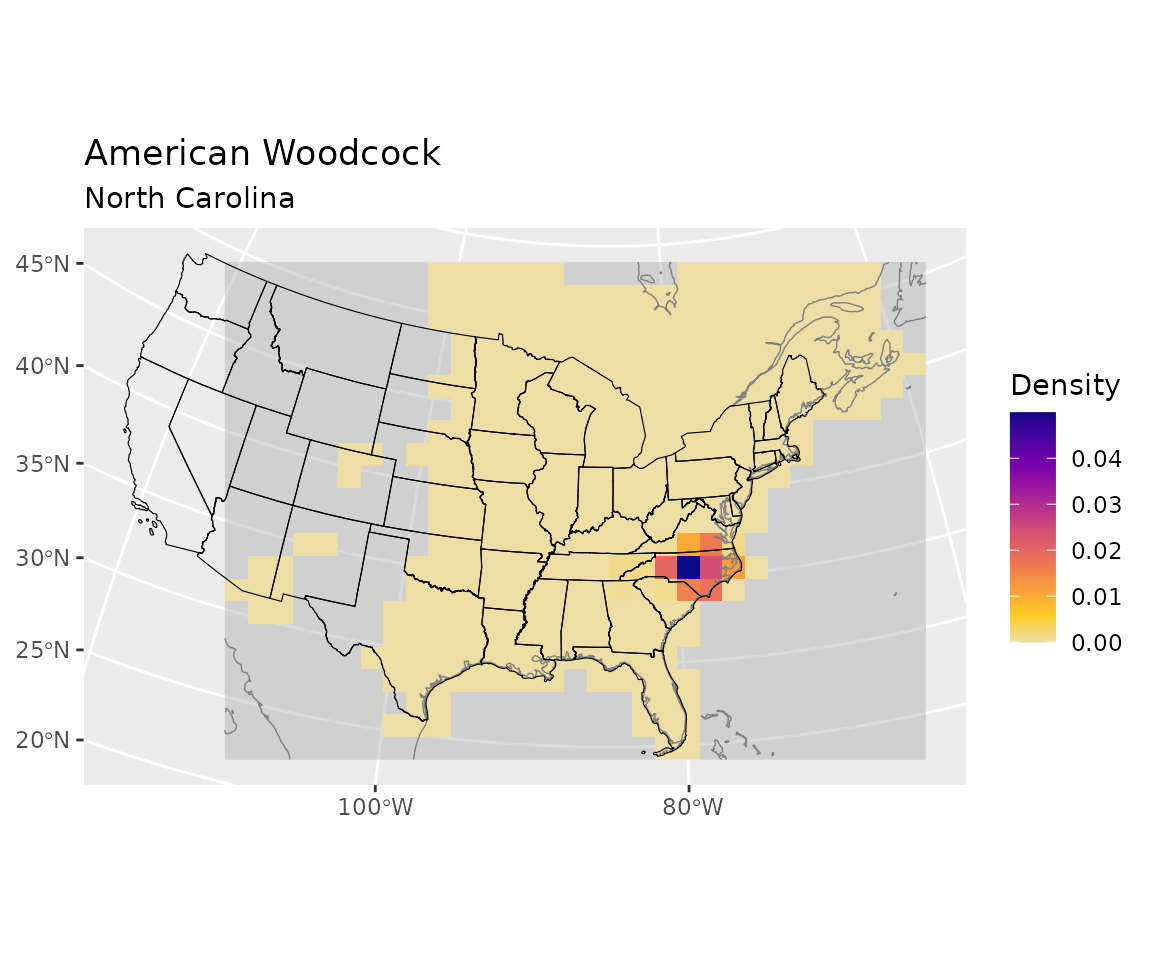

Project the distributions forward

Use BirdFlowR::predict() to project the distributions forward. With multiple input distributions the output will be a three dimensional array. Select the last element of the third dimension to get just the ending distributions in a matrix. The values in these distributions represent the proportion of the population that started in the corresponding polygon (columns) that ended in each active cell (rows).


# Project distributions forward to end date
pred <- predict(bf, distr = start_distr, start = start, end = end)

# Just keep last distribution 
end_distr <- pred[ , , dim(pred)[3]] 

# Preserve dimension names
dimnames(end_distr) <- dimnames(start_distr)

Visualize the ending distribution

This shows the ending distribution for the birds that started in North Carolina.

plot_distr(end_distr, bf, sel) +
  ggplot2::geom_sf(data = polys, 
                   inherit.aes = FALSE, 
                   linewidth = 0.2, 
                   color = "black", 
                   fill = NA)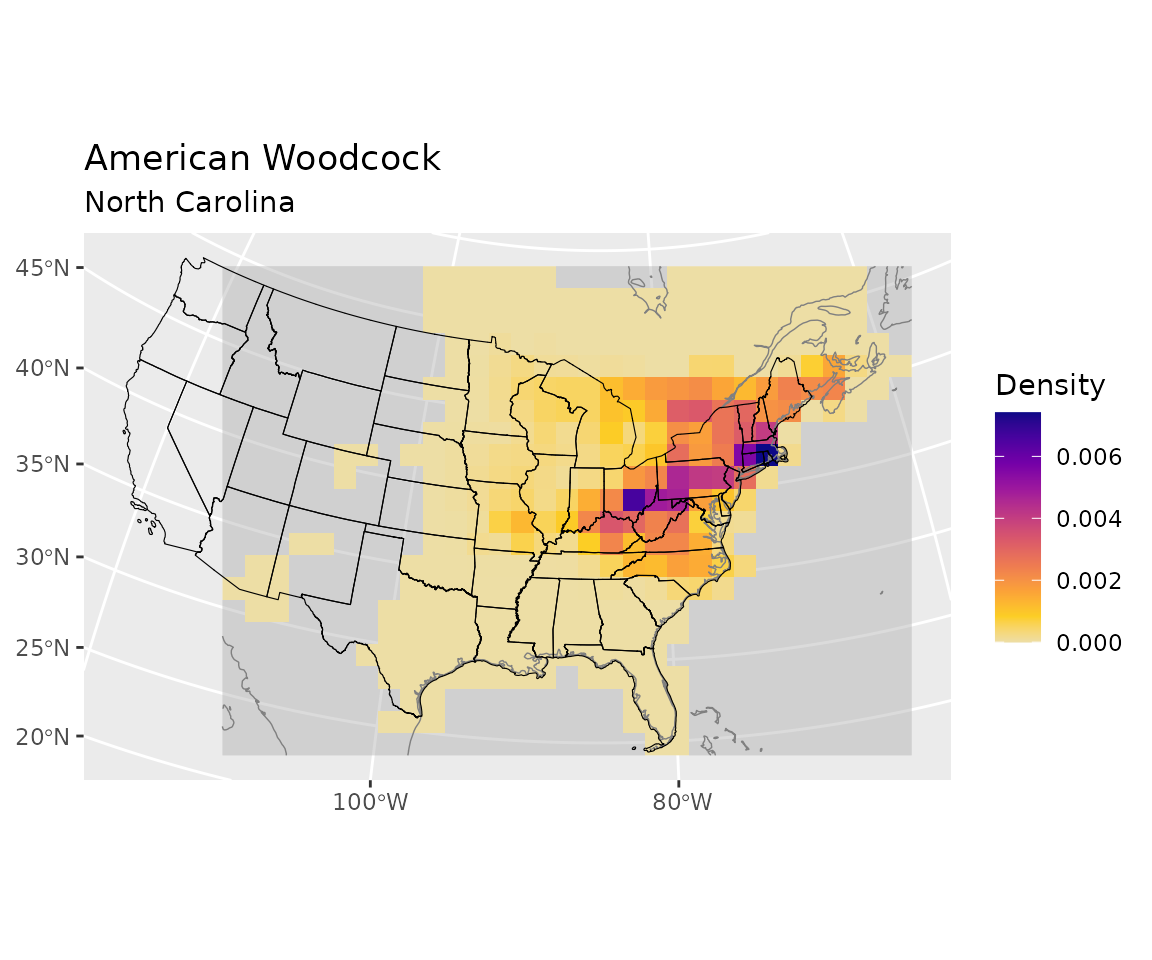

Collapse the ending cells into ending polygons

Convert the end_distr destination cells into destination polygons based on the overlap proportions in overlap.

The first “slow” way is perhaps easier to understand. The faster way produces the same result with matrix multiplication. Either way move is a matrix with rows for the starting polygons, columns for the destination polygons, and values that are the proportion of the population making the transition between the two.

slow <- FALSE
if (slow) {
  # Here we loop through each cell of the movement matrix filling in values
  # one by one.
  n <- nrow(polys)
  move <- matrix(NA, n, n, dimnames = list(from = polys$id, to = polys$id))
  for(from_i in seq_len(n)) for (to_i in seq_len(n)) {
    # Rows are source polygons, columns for destination polygons. 
    # Values are the proportion of the total population making the transition
    # between the corresponding polygons.
    move[from_i, to_i] <- sum(end_distr[, from_i] * overlap[, to_i])
  } 
} else {
  # Use matrix multiplication to do the same thing faster
  move <- t(end_distr) %*% overlap
  dimnames(move) <- list(from = polys$id, to = polys$id)
}

Visualize the polygonized end distribution

Plot the proportion of the total population that moved from
North Carolina to each each state.

polys$Proportion  <- move[sel, ]

gradient_colors <-
      c("#EDDEA5", "#FCCE25", "#FBA238", "#EE7B51", "#DA596A", "#BF3984",
        "#9D189D", "#7401A8", "#48039F", "#0D0887")

ggplot2::ggplot(data = polys) + 
  ggplot2::geom_sf(ggplot2::aes(fill = Proportion)) + 
   ggplot2::scale_fill_gradientn(colors = gradient_colors) + 
  ggplot2::ggtitle(paste0(species(bf), " movement from ", polys$id[sel]), 
                   subtitle = paste0(lookup_date(start, bf), " to ", 
                                     lookup_date(end, bf)))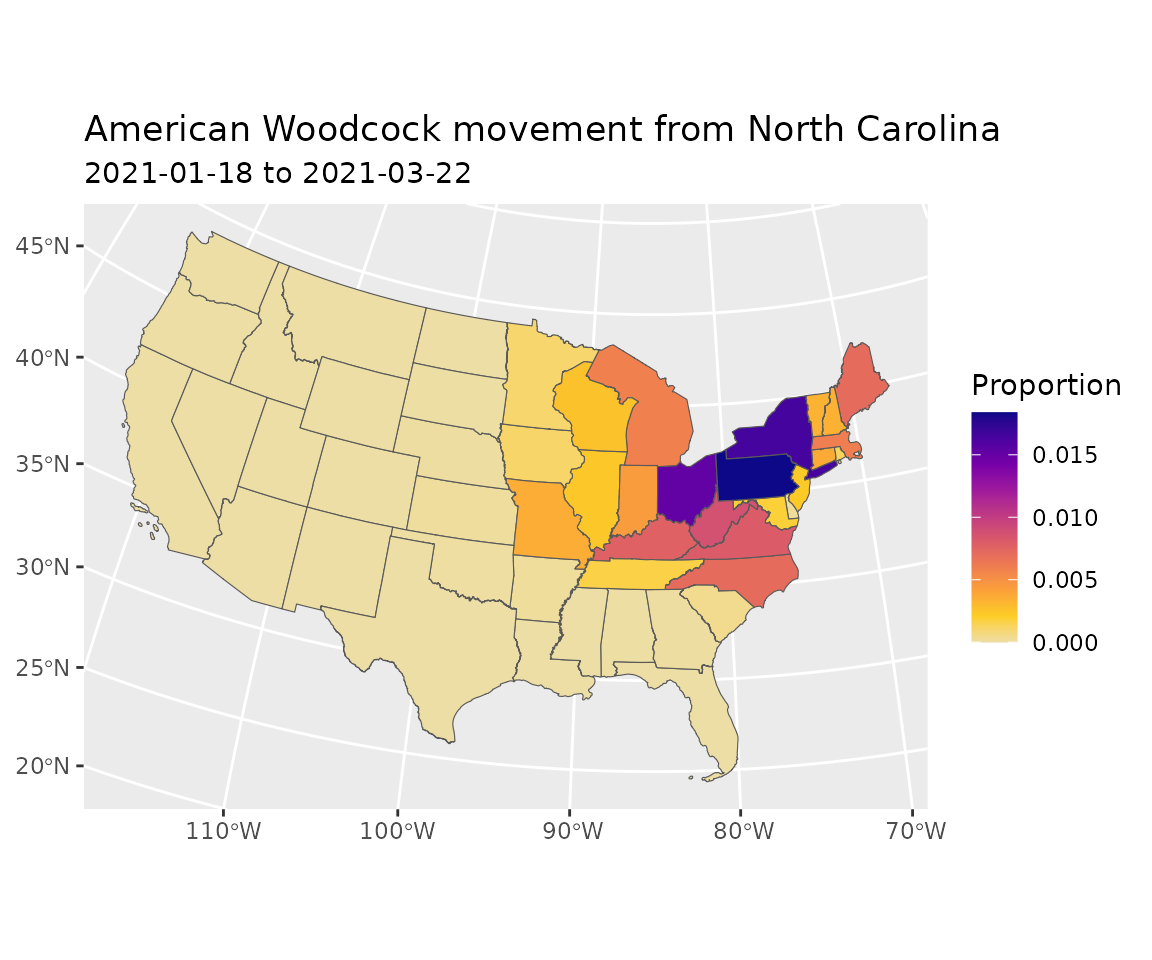

Adjust for population (optional)

You can multiply the movement by the total population of the species to estimated the number of individuals making each movement. This is likely necessary to aggregate or compare output across species.

# Convert to absolute numbers of Birds expected to move between 
# each pair of polygons
move_count  <- move * population

Adjust for area (optional)

Adjusting for area might be appropriate depending on the application. If the goal is to capture the total magnitude of movement between each source and destination polygon than do not adjust for area.

However, in our initial use case our points were in the specified states but did not represent the entire state so failing to adjust for state area would introduce a bias - essentially inflating movement for points that fell in bigger states. Similarly if you want an average per unit area movement between states that isn’t biased by state area you would adjust for area.

The adjustment is done by dividing the number of individuals moving between the two polygons by the area of each polygon in sq km to produce the expecting number to move between them per sq km at each end. Clearly, though this does not capture the fine scale variability within them some of which is captured in the original BirdFlow cells.


# Adjust for area if both the source and destination polgons
n <- nrow(polys)
from_area <- matrix(polys$sq_km, n, n, byrow = FALSE)
to_area <- matrix(polys$sq_km, n, n, byrow = TRUE)
move_area <- move_count / from_area / to_area

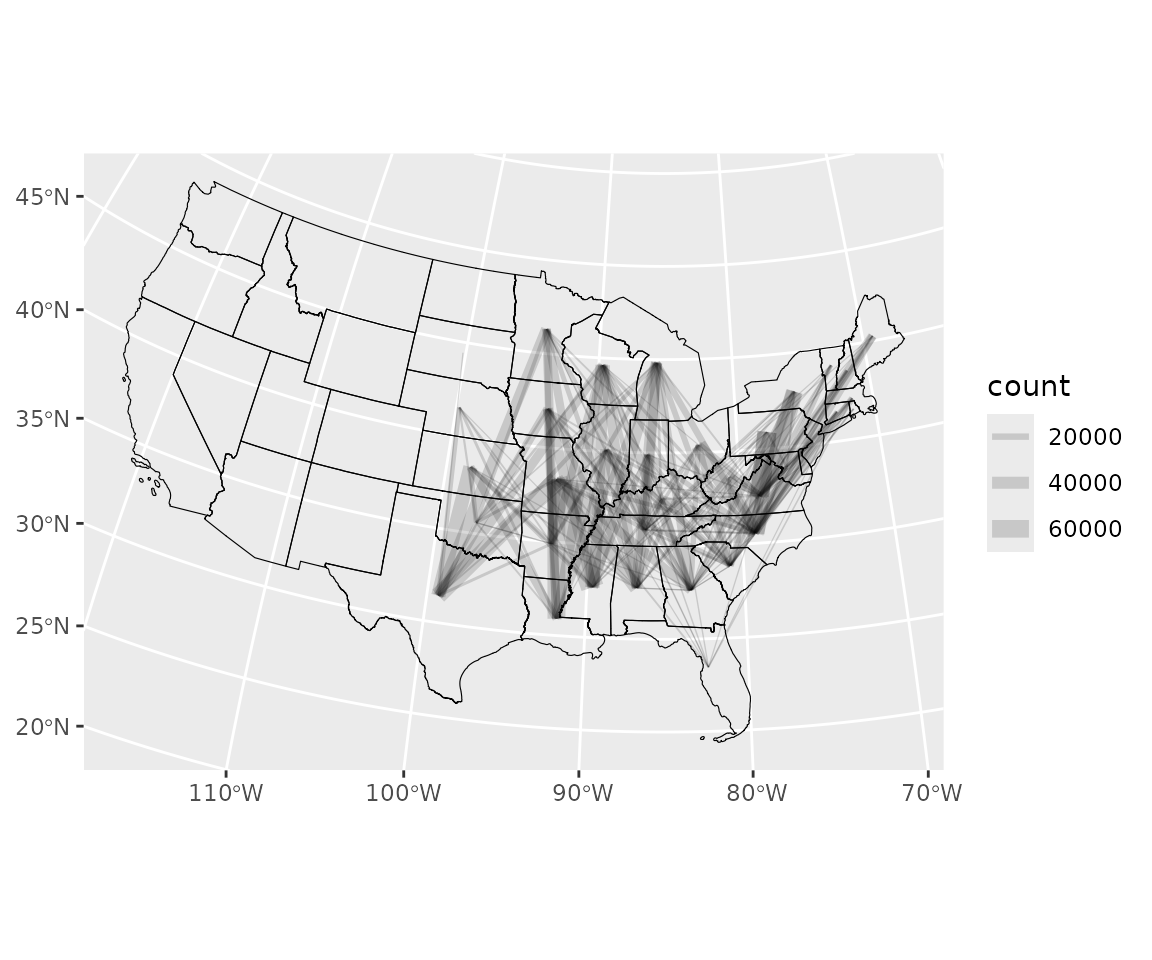
Visualize movement

plot_count_threshold <- 1000 # only plot lines for big movements

Plot non-zero estimated counts of birds moving between polygons and indicate magnitude with line thickness. Lines are only shown for movements of at least 1000 individuals.

n <- nrow(polys)
long <- data.frame(from =  rep(polys$id, times = n), 
                   to = rep(polys$id, each = n), 
                   count = as.vector(move_count))

# Add coordinates of centroids of to and from polygons
f_mv <- match(long$from, polys$id)
long$f_x <- polys$x[f_mv]
long$f_y <- polys$y[f_mv]
t_mv <- match(long$to, polys$id)
long$t_x <- polys$x[t_mv]
long$t_y <- polys$y[t_mv]

long <- long[long$count >= plot_count_threshold, ]

ggplot2::ggplot(long) + 
  ggplot2::geom_segment(ggplot2::aes(x = f_x, y = f_y, 
                                     xend = t_x, yend = t_y, 
                                     linewidth = count),
                        color = rgb(0, 0, 0, .15)) + 
  ggplot2::scale_linewidth(range = c(0.2, 4)) + 
  ggplot2::theme(axis.title = ggplot2::element_blank(),
                 strip.background = ggplot2::element_blank()) +
  ggplot2::geom_sf(data = polys, 
                   inherit.aes = FALSE, 
                   linewidth = 0.2, 
                   color = "black", 
                   fill = NA)